Simple Harmonic Motion of a Vertical Spring

L145. Simple Harmonic Motion of a Vertical Spring

This lab is divided into several parts. You must complete the parts in order.

Part A. Review of L123

Review the theory and methods of L123: Hooke's Law and a Measurement Spring Constant. Also review your original submission of that lab on WebAssign. If the teacher requested that you revise the analysis, you must do that before proceeding with L145, part B.
Complete WebAssign L145A.
Wait for the teacher's response to that assignment before continuing with Part B.

Part B. Period of a spring

Goal

To measure the period of a spring in oscillation to 3 significant figures and compare to theory

Prelab

Check your feedback from the instructor on L145A. If rework is required, do that and resubmit your work before continuing with Part B. You'll need an accurate value of the spring constant to continue with Part B.

Equipment

The same spring and spring support that you used in L123
Weight hanger
Slotted mass of 200 g
Stopwatch: You may use this program or a hand-held stopwatch that reads to 0.01 s. Do not use a sonic ranger or photogate for measuring time in this part of the lab.
Tape

Method

Sub-part 1

Enter your responses to items 1-5 in the WebAssign form L145B1. The items below are repeated on the form.

Enter the spring constant that you submitted in L145A. This should be the revised value if you did the analysis over. Give the number to 3 significant figures in SI units.
Place a total of 0.250 kg, including the weight hanger, suspended from the spring. Tape the weight hanger to the spring and the weight to the weight hanger. This will prevent the weight hanger and/or weight from bouncing off the spring to the floor. While this wouldn't damage the weight, it could break the weight hanger. It could also leave a dent in a wooden or lineoleum floor or crack a tile floor. You could also put a cushion on the floor just in case.
Keep the weight constant throughout this part of the experiment. Set the spring into oscillation by lifting it up--but not so much as to completely relax the spring--and releasing it. A lift of a few centimeters is sufficient. You'll use the stopwatch to measure 5 trials of the time for 1 complete cycle of the motion. (That's 1 cycle; not 2, or 3, or more.) Before you start taking measurements, read the following important note. Then take your 5 trials and record results to a precision of 0.01 s.

Do not practice your measurement technique and do not discard measurements. We know this is a crude measurement technique, but you need this information in order to later refine your technique appropriately. This is not a contest to see how close you can get to the same value every time.

Calculate the mean of your set of 5 measurements.
Calculate the percentage mean deviation of your set of 5 measurements. Round your result to 1 significant figure. In order to minimize rounding error, carry through all calculations of averages and deviations on your calculator and avoid rounding to the last step. If you know how to use formulas in Excel, this is a good way to do your calculations.
It should be obvious that your measurements don't meet the goal of the experiment. For a 3 significant figure measurement, you'll need to get the percentage mean deviation down to 1%. How many consecutive cycles N must you time in order to achieve that? Consider that the N cycle method divides the percentage mean deviation of the one cycle method by N.

Sub-part 2

Before continuing with this part, wait for the teacher's emailed response to Sub-part 1. Use WebAssign L145B2 to post your responses to the following.

The teacher will confirm the value of N that you will use for your next set of measurements. Enter that value. WebAssign will use it in checking your calculations.
Take a new set of 5 trials of the time for N cycles.
Calculate the mean of your set of 5 measurements.
Calculate the percentage mean deviation of your set of 5 measurements to 1 significant figure.
Now, using your result from step 3, calculate the period of the oscillation to 3 significant figures.
Assuming that the period, T, of an oscillating mass on a spring depends only the spring constant, k, and the mass, m, determine the mathematical combination of k and m that gives the right units for period. This result should be correct to within a constant numerical factor, which will be determined later by experiment. That is, you'll determine an equation of the form T = Cf(k,m), where f(k,m) is a function of k and m, and C is a numerical constant to be determined later. Give the function f(k,m) and show that the units reduce to those expected for period.
Using your measured spring constant, mass and period, and your formula above, calculate the numerical constant in your formula for period. Give the result.
Theoretically, what should the constant be? Look this up if you need to.
Calculate the experimental error between the calculated and theoretical values of the constant. Take the theoretical value to be accepted.
Describe 2 possible and significant sources of experimental error. Be specific in describing how the source could contribute to error. As always, phrases like human error and rounding error are not acceptable.

Part C. Equation of motion of the oscillating mass

Goal

To determine the equation of motion of a mass oscillating on a spring

Prelab

Complete and submit the previous parts of L145.

Equipment

The same spring and spring support that you used in the previous parts of the lab
Weight hanger
Slotted mass of 200 g
Computer with available USB port
LabQuest Mini interface and USB cable
Vernier Motion Detector 2 and cable

Method

Enter your responses in the WebAssign L145C form. The items below are repeated on the form.

Enter the following items for reference.
1. spring constant in SI units
2. mean period that you determined in Part B2
Place a total mass of 0.250 kg on the spring. This includes the weight hanger. Connect the motion detector and position it on the floor under the weight hanger as you did in L123. Start the Logger Pro software and then do the following.
1. Go to Experiment Menu, Data Collection, Collection tab, and change the sampling rate to 30 samples/sec. Also, set the experiment length to 3 seconds. Click OK.
2. Delete the velocity vs. time graph so that you only have position vs. time. Click Page -> Auto Arrange to maximize the graph size.
3. Set the spring into oscillation as you did in L145B. Click Collect to start data collection. You should obtain a smooth, sinusoidal graph. You may need to click the autoscaling icon at the top. There may be stray points toward the end of the time interval if the spring starts to sway from side to side.You may also find that the amplitude decreases significantly with time. If your graph shows evidence of either of these, just collect new data until you get a good-looking graph.
4. Save your file and upload it to WebAssign under item 2 of the L145C assessment form.

Next you'll determine the equation of the function that you just saved. That means you'll need to determine the equilibrium position, the amplitude, the period, and the phase shift. You should have already practiced these things. One method you may not use at this point is a curve fit. That would sidestep the knowledge that this lab expects you to demonstrate.

Describe the methods that you will use to determine the indicated characteristics below.
1. equilibrium position
2. amplitude
3. period (Use the position vs. time graph rather than the value that you determined in Part B2 of the lab.)
4. phase shift
Now carry out your methods. Be sure to have your calculator in radians mode. Give final values below to 3 significant figures.
1. equilibrium position
2. amplitude
3. period
4. phase shift (Assume a cosine function for the waveform.)
Write the equation of the position vs. time function. Use the same values that you gave above.
Perform the following checks on your equation. Substitute the time coordinate for one of the data points into your equation to see if you get the correct position. Enter the following:
1. time coordinate that you selected
2. position coordinate calculated from your equation (remember to have your calculator in radians mode)
3. position coordinate read from your graph
4. percentage difference between items b and c (give absolute value)
5. percentage difference between the period measured in Part L145B2 and that measured from your graph (give absolute value)

Part D. Position, velocity, and acceleration as a function of time

Goal

To examine the position, velocity, and acceleration of the spring as a function of time

Equipment

Use the same equipment as in L145C. In addition, you'll need the 100 g slotted mass.

Method

Collect your data as follows:

Suspend a total of 350 g of mass from the spring, including the weight hanger.
You'll need position, velocity, and acceleration vs. time graphs to be displayed in Logger Pro. Insert any graphs that you need, and make sure that the axis labels are appropriate. Auto-arrange the page so that the graphs don't overlap.
Go to Experiment, Data Collection, Collection tab, and set the experiment length to 2 seconds and the sampling rate to 30 samples/sec. Press OK.
Set the mass into oscillation and collect data.
You should get a smooth curve for the position graph, but the velocity and acceleration graphs may show some scatter in the points. (This has to do with the method used to calculate velocity and acceleration from the position data.) Select View, then Autoscale if the curves are not showing on any of the graphs. Then collect data as before.
Obtain a curve fit to each of the graphs as follows: Select Analyze, then Automatic Curve Fit, then Sine.
Save your file and upload it to item 1 of the WebAssign L145D form. You'll use the file in the instructions to follow.

Analysis

For the following, use your Logger Pro file with the fits to the position, velocity, and acceleration vs. time graphs. Enter your answers on the L145D WebAssign form. The questions are repeated below for reference.

Note: While the textbook makes a point of distinguishing between the terms angular velocity and angular frequency, they are both defined by ω = 2π/T. We will use the term angular velocity in the following.

Enter all values to 3 significant figures unless indicated otherwise.

Angular velocity and period
1. What fit coefficient represents the angular velocity in all of the fits?
2. Give the value of the angular velocity obtained from the fit coefficient for the position vs. time fit.
3. Use the angular velocity from the previous item to calculate the period of the mass on the spring.
4. Use the graph (not the fit) to determine the period of the mass on the spring. Describe the method that you use to achieve an accurate result. (Consider how you increased the accuracy of the measurement of period in L145B2.)
5. Now give the value of the period that you determined from the graph (not the fit).
6. Calculate the experimental error between the two values of period given above. Use the value obtained from the fit as the accepted value.
Comparision of angular velocity values
1. There's another way to determine the angular velocity. Calculate the angular velocity using the spring constant and the mass.
2. Calculate the experimental error between the values of angular velocity in 1b and 2a. Use the former value as accepted.
Position characteristics
1. Which two coefficients do you need from the fit to the position graph in order to determine the amplitude and equilibrium position of the motion?
2. Give the values of the fit coefficients that represent the amplitude and equilibrium position.
Velocity characteristics
1. Which direction is positive, up or down? (The answer isn't an arbitrary choice, because it's determined by the position of the sonic ranger and how the Logger Pro software records position.)
2. When the mass has its greatest positive displacement, what value do you expect for the velocity?
3. When the mass is passing the equilibrium position going down, do you expect the velocity to be positive or negative?
4. Does your velocity graph agree with your predictions?
Acceleration characteristics
1. When the mass has its greatest positive displacement, is the acceleration positive or negative?
2. If the mass were oscillating horizontally so that the only horizontal force on the mass was the spring force, why would one expect that when the mass had its greatest positive displacement, the acceleration would have its greatest negative value? Use Newton's 2nd Law and the defining relationship of simple harmonic motion in your answer. See section 13-2 if necessary. (We will see later that the vertically-oscillating system can, in fact, be treated the same as a horizontally-oscillating system.)
3. Assuming now that the vertically-oscillating system can be treated the same as a horizontally-oscillating system, what value would you expect the acceleration to be as the mass passed the equilibrium position going down?
4. Does your acceleration graph agree with your prediction?
Tension characteristics: While you don't have data for the tension force of the spring on the mass as a function of time, you can make sensible predictions below.
1. What direction is the tension at all times? Why is this expected?
2. What value do you expect for the tension when the mass is in equilibrium?
More about acceleration
1. What one coefficient from your fit to the Acceleration vs.Time graph can be used to determine the maximum and minimum values of the acceleration?
2. Give the value of the coefficient.
3. Given your result from part b and a law of physics, determine the maximum and minimum values of the net force.

Draw force diagrams for these three situations: i) mass displaced above equilibrium position, ii) mass at the equilibrium position, iii) mass displaced below the equilibrium position. Show the force vectors with approximately correct relative magnitudes. Refer to your diagrams as you answer the following.

More about tension
1. The magnitude of the tension force is _____ (less than, equal to, more than) the weight when the object is displaced above the equilibrium position.
2. The magnitude of the tension force is _____ (less than, equal to, more than) the weight when the object is displaced below the equilibrium position.
3. The net force on the object is _____ (up, down) when the object is displaced above the equilibrium position.
4. The net force on the object is _____ (up, down) when the object is displaced below the equilibrium position.
Net force
1. Assuming +x is up, write the one net force equation that applies to the object in all positions while oscillating vertically. Use the symbols T, m, and g.
2. Using the net force equation and the maximum and minimum values of the net force from 7c, calculate the maximum and minimum values of the tension.

Part E. Net Force and Energy Analysis

This part is primarily theory. There's no data to take, although you'll use a result from L145D. Write your responses on paper and submit your scanned file to BrainHoney.

Goal

To show that a net force and energy analysis for a vertically-oscillating spring yields the same results as for a horizontally-oscillating spring

Force analysis

Open and run this animation to familiarize yourself with the situation.

The diagram below shows 4 side-by-side snapshots (numbered 1-4) of the system. Here are the situations represented in each snapshot:

Snapshot 1: The spring is motionless with no added mass.
Snapshot 2: Total mass m has been added to the spring. The system is in equilibrium. The equilibrium position is assumed to be 0.
Snapshot 3: The mass is moving either up or down, and has a positive displacement y from the origin. The direction of +y is defined to be up.
Snapshot 4: The mass is moving either up or down, and has a negative displacement y from the origin.

Also note the following:

The displacement of the bottom of the spring from the origin in Snapshot 1 is defined to be y₁. This is a positive displacement.
y is the position variable. As such, it can have positive, 0, or negative values.

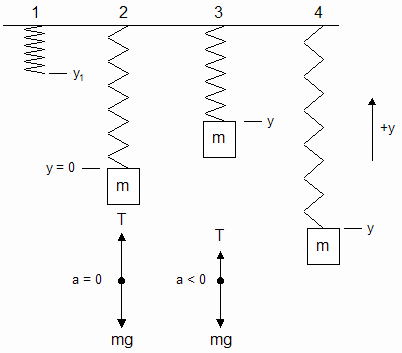
Now we'll do a net force problem for Snapshot 2. Refer to the force diagram associated with Snapshot 2 above.

Net force analysis for Snapshot 2
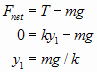	The net force equation is written.
	There is no acceleration, so the net force is 0. Hooke's Law is used to substitute ky₁ for T. Note that the value of ky₁ is positive as expected with +y pointing up.
	y₁ is solved for. This gives us an expression for y₁ that will be useful later.

Next we'll do a net force problem for Snapshot 3. Once again, refer to the force diagram above associated with Snapshot 3. The tension force is now less than the weight, and the acceleration is down. We'll make an exception to the usual practice of selecting the positive direction to be that of the acceleration. The reason for this exception is to keep the direction of positive displacement the same for all snapshots. Otherwise, sign inconsistencies would result.

Net force analysis for Snapshot 3
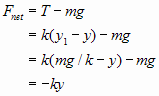	The net force equation is written.
	Since y₁ and y are both positive in this case, the quantity (y₁ - y) < y₁. This results in a smaller tension force than for Snapshot 2.
	The result obtained for y₁ from the analysis of Snapshot 2 is substituted.
	Since k and y are positive, the net force is negative. This is consistent with a downward (negative) acceleration.

The last result shows that F_net is proportional to the displacement from the equilibrium position. There is no dependence on g. Hence, we can analyze this system for forces as if it were a horizontally-oscillating spring. Note that in this situation the equilibrium position is not the unstretched position of the spring. Rather, the equilibrium position is the position shown in Snapshot 2.

Problems for You to Do

Following the guide of the net force analysis for Snapshot 3, do the net force analysis for Snapshot 4. Start with the relevant force diagram. Consider the following questions in order to avoid sign mistakes. You don't have to write the answers to the questions, but you do have to show a net force analysis similar to what was done above.
1. Does y represent a positive or negative number for this analysis?
2. Is (y₁ - y) less than or greater than y₁?
3. Does F_net point up (positive) or down (negative)?
Using the default data in the applet and results of the force analyses above, calculate the following. Show your work.
1. spring constant
2. maximum and minimum values of the tension force
3. maximum and minimum values of the acceleration of the mass

Energy analysis

Goal: For the vertically-oscillating spring, derive an equation for the velocity of the mass as it passes through y = 0 in terms of the amplitude of the motion, the spring constant, and the mass on the spring.

Introduction: We'll take the system for the conservation of energy analysis to be the spring, mass, and Earth. We'll continue to use the same coordinate system as for the net force analysis. These are the states:

initial: the mass as it's passing through y = y_i = 0 on the way down
final: the lowest position of the mass, y_f = -A. The negative sign is necessary, because the amplitude A is defined to be positive.

Since we've defined the system in such a way that there are no external forces, the conservation of energy equation that applies is 0 = ΔE_sys.

Energy term	Formula	Sign
K_i
K_f
U_gi
U_gf
U_ei
U_ef