L125. Acceleration on a Swing

A tabletop version of the State Fair ride, the Giant Swing, will be used to study acceleration in circular motion. Here's a video clip of the State Fair ride. For the latter, the axis of rotation nutates, that is, it has a nodding motion. That makes for a more interesting ride than if the axis were stationary. The tabletop version used in the present lab doesn't nutate. That keeps the analysis simpler.

Goals

To determine--in two different ways--the acceleration of a passenger in rotational motion on a swing
To determine the ratio of the apparent weight to the true weight of the passenger.

Introduction

In the toy airplane exercise V108, you used two different methods to determine the speed of the airplane. One of these was a kinematical method that used the definition of speed. The other was a dynamical method that used a force analysis. In this lab, you'll use both kinematical and dynamical methods to determine the acceleration of the liquid-filled canister on the tabletop swing. Then you'll determine how much heavier the passenger appears to be than its true weight.

Preparation for the WebEx session

Do items a-g in advance of the WebEx session.

View the video, Acceleration on a Swing.
Review the analysis presented in the toy airplane video of V108.
Click on the photo in the Theory section below. (This larger version has inverted black and white tones.) Print the photo.
Have your protractor available.
Make sure you have a working version of Logger Pro on your computer.
Download this video clip to use for analysis.
Complete the Theory below by entering your responses in L125PL.

Theory

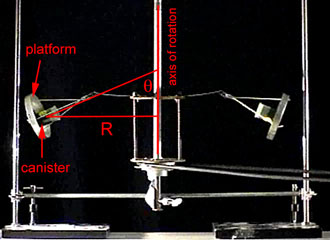Refer to the annotated photo to the right for the definitions of the radius, R, of the path of the canister on the left and the angle, θ, that the canister makes with the axis of rotation. The analysis below will be for the left canister. A similar analysis is assumed to apply to the other canister. Other symbols that will be used in the theory include the mass, m, of a canister and the period of rotation, T, of a canister about the axis.

Determine an equation for the acceleration, a, of the canister in terms of R and T and fundamental constants only.
State the direction of the acceleration of the left canister when in the position shown in the photo.
Let N represent the normal force exerted by the platform on the canister. In order to simplify the analysis, assume that the vertical component of N is sufficient to balance the weight, mg, of the canister. Thus, you'll ignore any static frictional force exerted by the platform on the canister. Draw the force diagram for the canister and show the directions you select for positive displacement.
Write the net force equations for the canister.
Solve the net force equations simultaneously for the acceleration of the canister in terms of g and θ only.
Use one of the net force equations to solve for the ratio of normal force to weight, N/(mg), in terms of θ only.

The remainder of the lab will be available later.