Part A. Introduction

As you read through this introductory material, there will be some questions to answer. Write your answers in WebAssign L120A.

If several forces act on an object that is either at rest or moving at constant velocity, then the forces must add to zero. That is, there is 0 net force. This is simply another way of stating Newton's 1st Law. If you know the magnitudes and directions of the forces, then you can add them as vectors to show that the result is zero. 

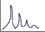
Suppose three strings are tied together in a knot and then the strings are pulled in 3 different directions as shown in the photo below. If the knot is held motionless, then the strings are in equilibrium, and the forces should add to zero. We can show this to be true by using either graphical or component addition of the force vectors.

Graphical Addition

1. Let's represent the three forces by vectors A, B, and C  as shown in the figure below.

1. On the PencilPad in WebAssign, redraw the three force vectors in a head-to-tail arrangement. Specifically, move the tail of vector B to the head of vector A and the tail of vector C to the head of vector B. Label the vectors.
2. In the text window below the PencilPad, write in a sentence how you can tell from the head-to-tail diagram whether the forces are in equilibrium.

Component Addition

2. Suppose that the three forces have the following magnitudes and direction angles measured counterclockwise from the +x-axis.

Force	Magnitude (N)	Direction angle (°)
A	6.32	18.4
B	8.50	118.0
C	9.70	258.0

1. Calculate the x-and y-components of the forces and enter them in the table in WebAssign. Then calculate the components of the net force.
2. Based on your calculations, how can you tell that the three forces are in equilibrium?

Required materials for Part B

3. When you do Part B of the lab, you'll need to have these materials available: 30-cm ruler, protractor, this photo. Print the photo now.